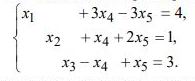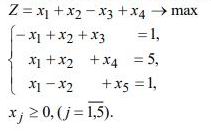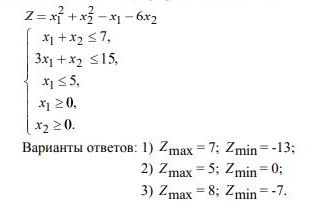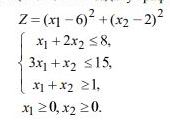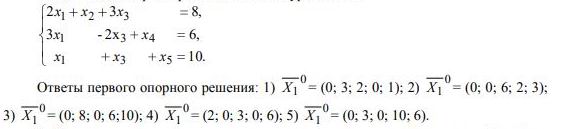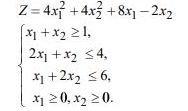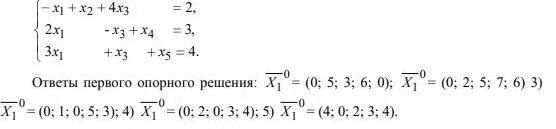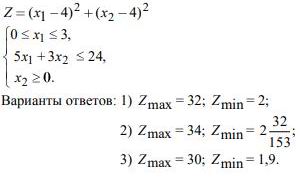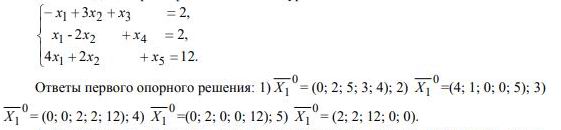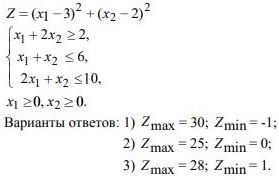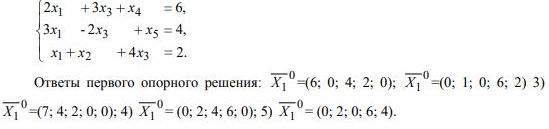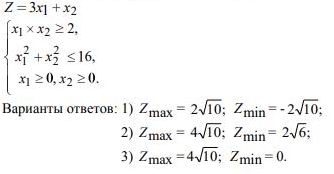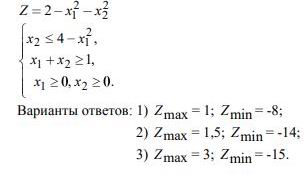Контрольная работа по предмету: Методы оптимальных решений. Вариант 2

Контрольная работа по предмету: Методы оптимальных решений. Вариант 2

1. Если в оптимальном плане М-задачи хотя бы одна искусственная переменная …, то система ограничений исходной задачи несовместна в области допустимых решений.

2. Найти два опорных решения системы:

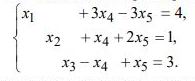
Ответы первого опорного решения:
1) 0X1= (0; 1; 3; 4; 1); 2)0X1= (3; 0; 1; 0; 1); 3)0X1= (4; 1; 3; 0; 0); 4)0X1= (0; 3; 0; 2; 1);
5)0X=(6; 0; 2; 0; 3).

3. Решить исходную задачу симплексным методом, составить к ней
двойственную, найти оптимальное решение двойственной задачи.
Z=x1+x2-x3+x4_max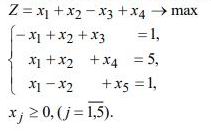

4. На предприятии имеются 4 вида ресурсов и выпускает 4 вида продукции. Все данные задачи заданы в таблице.
Вид ресурса    Затраты ресурсов на 1 единицу продукции Запас
                                  1 2 3 4
В1                             5 4 6 3 600
В2                             3 1 4 2 450
В3 0 5 3 7 700
В4 4 1 5 4 520
Цена 1 единицы
продукции             7 4 5 8
Найти оптимальный план выпуска продукции при котором прибыль отреализации продукции будет максимальной.
Требуется:
а) Составить математическую модель исходной и двойственной задач.
б) Записать оптимальный план исходной задачи ,
в) Записать оптимальный план двойственной ,
г) Проанализировать решение задачи с помощью свойств двойственных оценок (4 свойства).
д) На сколько изменится, целевая функция в оптимальном плане, если дополнительно приобрести 300 единиц первого ресурса.
Ответы: 1)Zmax=36,75; 2)Zmax=24,79; 3)Zmax=129,06; 4)Zmax=125,38; 5)Zmax=300.
К задаче прилогается распечатка решения на ЭВМ.
Распечатка к задаче № 4.
Module/submodule: Linear Programming
Problem title: ( untitled)
Objective: Maximize
Results -----------------

5. Решить транспортную задачу
ai = (130, 170, 150, 50)
bj = (100, 90, 150, 90, 70)
8 3 1 5 2
2 9 6 4 3
1 6 4 5 4
6 5 7 8 2
Ответы: 1)Zmin=740; 2)Zmin=1380; 3)Zmin=670; 4)Zmin=1200; 5)Zmin=1580.

6. Найти критический путь и его длину, полный резерв времени работы (2-5).

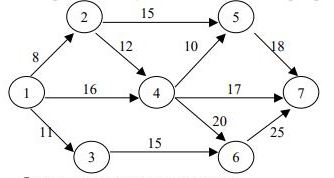
Ответы длины критического пути: 1) 70; 2) 65; 3) 80; 4) 78; 5) 68.

7. В области решений системы неравенств определить глобальные экстремумы
функций. Решить задачу графическим способом

Варианты ответов:
1)Zmax= 7; Zmin= -13;
2)Zmax= 5; Zmin= 0;
3)Zmax= 8; Zmin= -7.

Мы так же можем выполнить для вас любой другой вариант, для этого напишите нам: zakaz@referatch.ru

ВАРИАНТЫ ЗАЧЕТНЫХ ЗАДАНИЙ

Вариант 1
1. Множество точек n-мерного пространства называется выпускным, если любые две точки данного множества можно соединить отрезком, который …. данному множеству.

2. Найти два опорных решения системы
Ответы первого опорного решения:
1)0X1= (3; 1; 4; 3; 2),
2)0X1= (4; 0; 5; 0; 2),
3)0X1= (4; 2; 5; 0),
4)0X1= (7; 0; 1; 2; 0),
5)0X1= (2; 0; 5; 0; 4).

3. Решить исходную задачу симплексным методом, составить к ней модель двойственной задачи, найти оптимальное решение двойственной задачи. Z=4x1+5x2_max

4. На предприятии имеется 4 вида ресурса и оно выпускает 4 вида продукции.Исходные условия задачи заданы в таблице.
Таблица данных
Вид ресурса   Затраты ресурсов на 1 единицу продукции Запас
                                   1 2 3 4
В1                              5 3 4 2 730
В2                              4 0 5 1 450
В3                              0 6 3 4 600
В4                              4 1 3 5 540
Цена 1 единицы
продукции                          7 6 2 9
Найти оптимальный план выпуска продукции при котором прибыль от реализации
продукции будет оптимальным.
Требуется:
а) Составить математическую модель исходной и двойственной задачи и двойственной к ней.
б) Записать оптимальный план исходной задачи ,
в) Записать оптимальный план двойственной задач
г) Проанализировать решение задачи с помощью свойств двойственных оценок (4 свойства).
д) Можно ли спрогнозировать изменение целевой функции в отчетном плане,
если дополнительно приобрести 100 ед. четвертого ресурса, если можно, то на сколько
изменится целевая функция (Zmax) при этом величину изменения обозначайте Zmax .
Ответы: Zmax 1) 56,9; 2) 115,38; 3) 47,69; 4) 0.
К задаче прилагаются распечатки решения на ЭВМ.
Распечатка к задаче № 4.
Module/submodule: Linear Programming
Problem title: ( untitled)
Objective: Maximize
Results -----------------

5. Решить транспортную задачу.
ai = (170, 130, 150, 200),
bj = (100, 190, 150, 130, 80),
3 9 5 4 3
8 3 4 2 5
2 6 4 5 4
5 6 8 7 2
Ответы: 1) Zmin = 1200; 2) Zmin = 400; 3) Zmin = 7200; 4) Zmin = 2390; 5) Zmin = 8640.

6. Найти критический путь, длину критического пути и свободный резерв
времени работы (3-6).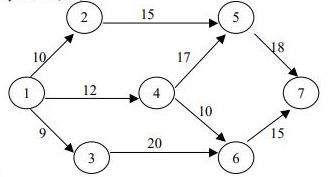

Ответы длины критического пути: 1) 50; 2) 46; 3) 40; 4) 47.

7. В области решений системы неравенств определить глобальные экстремумы
функций. Решить задачу графическим способом. Z=(x1-6)+(x2-2)

Варианты ответов: 1) Zmax= 37; Zmin= 2,6; 2) Zmax= 40; Zmin = 2,5; 3) Zmax= 42; Zmin= 2,4.

Вариант 3
1. Признаком существования альтернативного оптимума при расчете по симплексным таблицам является наличие …?
2. Найти два опорных решения системы уравнений.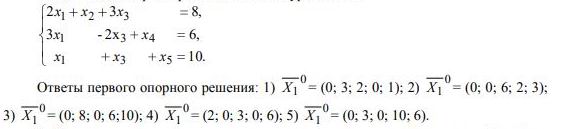

Ответы первого опорного решения:
1)0X1= (0; 3; 2; 0; 1);
2)0X1= (0; 0; 6; 2; 3);
3)0X1= (0; 8; 0; 6;10);
4)0X1= (2; 0; 3; 0; 6);
5)0X1= (0; 3; 0; 10; 6).

3. Решить исходную задачу симплексным методом, составить к ней модельдвойственной задачи, найти оптимальный план двойственной задачи. Z= 2x4+x2_max

4. На предприятии имеется 4 вида ресурса и оно выпускает 4 вида продукции. Исходные условия задачи заданы в таблице.
Таблица данных
Вид ресурса    Затраты ресурсов на 1 единицу продукции Запас ресурса
                       1 2 3 4
В1                    3 0 3 1 550
В2                    1 5 2 6 350
В3                    4 1 3 2 600
В4                    1 6 2 3 520
Цена 1 единицы
продукции              5 4 3 2
Найти оптимальный план выпуска продукции при котором прибыль от реализации продукции будет максимальна.
Требуется:
а) Составить математическую модель исходной и двойственной задач.
б) Записать оптимальный план исходной задачи
в) Записать оптимальный план двойственной
г) Проанализировать решение задачи с помощью свойств двойственных оценок .
д) Как изменится , целевая функция в оптимальном плане , если цену первого вида продукции увеличить до 15?
Ответы: 1)Zmax 56,9; 2) )Zmax=550,2; 3) )Zmax=39,47; 4) )Zmax=1526,316; 5) )Zmax=921,5.
К задаче прилогается распечатка решения на ЭВМ.
Распечатка к задаче № 4.
Module/submodule: Linear Programming
Problem title: ( untitled)
Objective: Maximize
Results -----------------

5. Решить транспортную задачу
ai = (100, 120, 80, 200),
bj = (100, 150, 100, 75, 75),
7 5 3 2 1
3 4 8 4 5
2 2 5 6 9
1 3 6 5 8
Ответы: 1)Zmin=1840; 2)Zmin=1415; 3)Zmin=1250; 4)Zmin=895; 5)Zmin=1720.

6. Найти критический путь и его длину, полный резерв времени работы (2-5).
Ответы:1) 70; 2) 92; 3) 100; 4) 66; 5) 65.

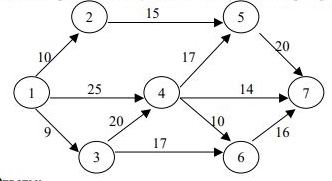
7. В области решений системы неравенств определить глобальные экстремумы функций. Решить задачу графическим способом. Z=4x1+4x2+8x1-2x2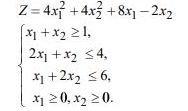

Варианты ответов: 1)Zmax= 30; Zmin= 1,875; 2)Zmax= 56; Zmin= 2,5; 3)Zmax= 32; Zmin= 2.111

Вариант 4
1. Решение системы линейных уравнений называется базисным, если ...обращаются в ноль.
2. Найти два опорных решения системы.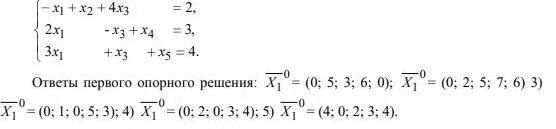

Ответы первого опорного решения:
0X1= (0; 5; 3; 6; 0);
0X1= (0; 2; 5; 7; 6) 3)
0X1= (0; 1; 0; 5; 3); 4)
0X1= (0; 2; 0; 3; 4); 5)
0X1= (4; 0; 2; 3; 4).

3. Решить исходную задачу симплексным методом, составить к ней модель
двойственной задачи и найти ее оптимальное решение.
Z=2x1-x2 =-3x3+x4_max

4. Предприятие имеет 4 вида ресурсов и выпускает 4 вида продукции. Исходные
условия задачи заданы в таблице.
Таблица данных
Вид ресурса   Затраты ресурсов на 1 единицу продукции Запас ресурса
                              1 2 3 4
В1                          4 20 5 2 560
В2                          3 1 3 5 250
В3                          0 5 8 3 600
В4                          4 2 2 4 520
Цена 1 единицы
продукции                    6 7 5 3
Найти оптимальный план выпуска продукции при котором прибыль от реализации продукции будет максимальной.
Требуется:
а) Составить математическую модель исходной и двойственной задач.
б) Записать оптимальный план исходной задачи
в) Записать оптимальный план двойственной
г) Проанализировать решение задачи с помощью свойств двойственных оценок .
д) Как изменится целевая функция в оптимальном плане, если цену первого вида
продукции увеличить до 20?
Ответы: 1)Zmax=606,6662; 2)Zmax=708,982; 3)Zmax=902,386; 4)Zmax=728,625; 5)Zmax=708,6662.
К задаче прилагается распечатка решения на ЭВМ.
Распечатка к задаче № 4.
Module/submodule: Linear Programming
Problem title: ( untitled)
Objective: Maximize
Results -----------------

5. Решить транспортную задачу
ai = (270, 230, 200, 250),
bj = (170, 210, 200, 170, 200),
4 5 7 4 3
9 8 10 8 4
3 4 6 7 5
8 7 8 5 4
Ответы: 1)Zmin=1925; 2)Zmin=8645; 3)Zmin=9725; 4)Zmin=9675; 5)Zmin=4750.

6. Найти критический путь его длину и определить свободный резерв времени работы (3-6)

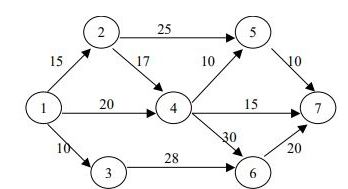
Ответы длины критического пути:
1) 82; 2) 95; 3) 79; 4) 84; 5) 100.
7. В области решений системы неравенств определить глобальные экстремумы функций. Решить задачу графическим способом.

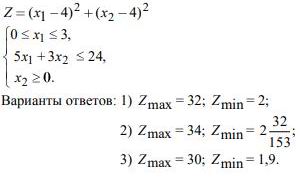
Варианты ответов: 1)Zmax= 32; Zmin= 2; 2)Zmax= 34; Zmin=2/153/32 3)Zmax=30;Zmin= 1,9.

Вариант 5
1. Каждому опорному решению системы уравнений задачи линейного программирования соответствует … множество допустимых решений системы ограничений.
2. Найти два опорных решения системы уравнений.

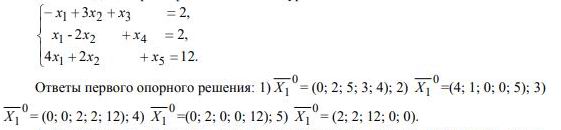
Ответы первого опорного решения: 1)0X1= (0; 2; 5; 3; 4); 2)0X1=(4; 1; 0; 0; 5); 3)0X1= (0; 0; 2; 2; 12); 4)0X1=(0; 2; 0; 0; 12); 5)0X1= (2; 2; 12; 0; 0).

3. Составить к исходной задаче двойственную. Решить исходную задачу симплексным методом, найти оптимальное решение двойственной задачи.
Z=2x1+3x2+2x3+x4_max

4. Предприятие имеет 4 вида ресурсов и выпускает 4 вида продукции. Исходныеусловия задачи заданы в таблице.
Таблица данных
Вид ресурса Затраты ресурсов на 1 единицу продукции Запас ресурса
                      1 2 3 4
В1                  3 0 3 1 400
В2                  4 2 5 2 550
В3                  0 5 2 6 650
В4                  4 1 3 2 520
Цена 1 единицы
продукции            6 5 7 9
Найти оптимальный план выпуска продукции при котором прибыль от реализации продукции будет максимальна.
Требуется:
а) Составить математическую модель исходной и двойственной задач.
б) Записать решение исходной задачи
в) Записать решение двойственной
г) Проанализировать решение задачи с помощью свойств двойственных оценок (4 свойства).
д) Как изменится, значение целевая функция в оптимальном плане, если дополнительно приобрести 100 единиц второго ресурса.
Ответы: 1)Zmax=25; 2)Zmax=125; 3)Zmax=100; 4)Zmax=120; 5)Zmax=45.
К задаче прилагается распечатка решения на ЭВМ.
Распечатка к задаче № 4.
Module/submodule: Linear Programming
Problem title: ( untitled)
Objective: Maximize
Results -----------------

5. Решить транспортную задачу
ai = (150, 200, 200, 210)
bj = (220, 170, 210, 150, 200)
14 8 5 4 6
13 10 4 10 6
16 11 8 8 7
10 7 6 12 11
Ответы: 1)Zmin=4350; 2)Zmin=742; 3)Zmin=1780; 4)Zmin=5620; 5)Zmin=978.
6. По сетевому графику найти ранний и поздний сроки свершения событий, определить критический путь и его длину, найти свободный и полный резерв времени работы (2-5).

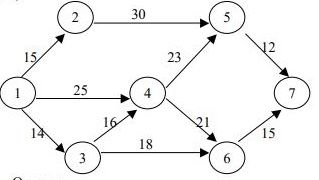
Ответы:1) 65; 2) 78; 3) 56; 4) 85; 5) 56.
7. В области решений системы неравенств определить глобальные экстремумы функций. Решить задачу графическим способом.

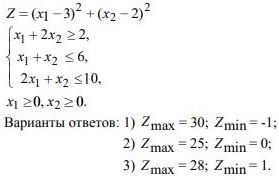
Варианты ответов: 1)Zmax= 30;Zmin= -1; 2)Zmax= 25;Zmin= 0; 3)Zmax= 28;Zmin= 1.116

Вариант 6
1. Путь ... связывающий начальное и завершающее события называется ...
2. Найти два опорных решения системы

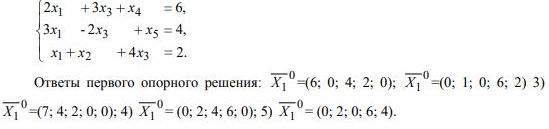
Ответы первого опорного решения:0X1=(6; 0; 4; 2; 0); 0X1=(0; 1; 0; 6; 2) 3)0X1=(7; 4; 2; 0; 0); 4)0X1= (0; 2; 4; 6; 0); 5) 0X1= (0; 2; 0; 6; 4).

3. Решить исходную задачу симплексным методом, составить к нейдвойственную, найти оптимальное решение двойственной задачи.
Z=2x1+4x2_max

4. Предприятие имеют 4 вида ресурсов и выпускает 4 вида продукции. Все данные задачи заданы в таблице.
Таблица данных
Вид ресурса Затраты ресурсов на 1 единицу продукции Запас ресурса
                      1 2 3 4
В1                  3 4 2 5 400
В2                  4 2 5 2 800
В3                  0 3 6 2 300
В4                  3 1 0 4 500
Цена 1 единицы
продукции             4 3 9 2
Найти оптимальный план при котором выручка будет оптимальной.
Требуется:
а) Составить математическую модель исходной и двойственной задач.
б) Записать оптимальный план исходной задачи
в) Записать оптимальный план двойственной
г) Провести анализ решения задачи с помощью свойств двойственных оценок (4
свойства).
д) Как изменится , целевая функция в оптимальном плане , если цену первого
вида продукции увеличить до 12?
Варианты ответов: 1)Zmax=56,9; 2)Zmax=1000; 3)Zmax=800; 4)Zmax=2100, 5)Zmax=920.
К задаче прилагается распечатка решения на ЭВМ.
Распечатка к задаче № 4.
Module/submodule: Linear Programming
Problem title: ( untitled)
Objective: Maximize
Results -----------------

5. Решить транспортную задачу
ai = (270, 350, 200, 230)
bj = (190, 210, 200, 230, 220)
10 9 5 5 4
12 7 3 4 5
6 5 10 9 3
8 4 6 7 6
Ответы: 1)Zmin=12170; 2)Zmin=4470; 3)Zmin=7125; 4)Zmin=3520; 5)Zmin=8746.

6. По сетевому графику найти ранний и поздний сроки свершения событий, определить критический путь и его длину, найти свободный и полный резерв времени

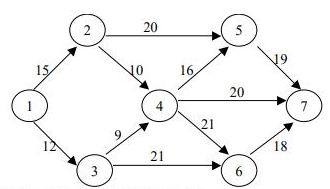
Ответы длины критического пути:
1) 70; 2) 87; 3) 64; 4) 60; 5) 65.

7. В области решений системы неравенств определить глобальные экстремумы функций. Решить задачу графическим способом Z=3х1+х2

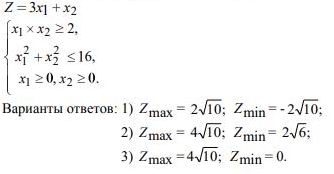
Варианты ответов: 1)Zmax=2 10; Zmin= - 2 10; 2)Zmax=4 10; Zmin=2 6; 3)Zmax = 4 10; Zmin= 0.

Вариант 7
1. Если в оптимальном плане М-задачи все искусственные переменные ..., то...решение будет оптимальным и в исходной задаче.
2. Найти два опорных решения системы

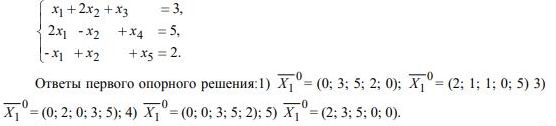
Ответы первого опорного решения:1)0X1= (0; 3; 5; 2; 0); 0X1= (2; 1; 1; 0; 5) 3)0X1= (0; 2; 0; 3; 5); 4)0X1= (0; 0; 3; 5; 2); 5)0X1= (2; 3; 5; 0; 0).

3. Решить исходную задачу симплексным методом, составить к ней двойственную, найти оптимальное решение двойственной задачи.
Z=2x1+3x2+5x3_max

4. Предприятие имеют 4 вида ресурсов и производит 4 вида продукции. Все данные задачи заданы в таблице. Таблица данных
Вид ресурса     Затраты ресурсов на 1 единицу продукции Запас ресурса
                                           1 2 3 4
В1                                         4 5 2 3 240
В2                                         3 2 5 4 250
В3                                         2 0 5 1 190
В4                                         2 6 1 3 300
Цена 1 единицы
продукции                                  9 12 5 8
Найти оптимальный план выпуска продукции при котором прибыль от реализации продукции будет максимальной.
Требуется:
а) Составить математическую модель исходной и двойственной задач.
б) Записать оптимальный план исходной задачи
в) Записать оптимальный план двойственной
г) Проанализировать решение задачи с помощью свойств двойственных оценок (4 свойства)
д) Как изменится , целевая функция в оптимальном плане , если дополнительно
приобрести 50 единиц второго ресурса.
Ответы: 1)Zmax=20,128; 2)Zmax=14,285; 3)Zmax=22,142; 4)Zmax=13,178; Zmax=25,642.
К задаче прилогается распечатка решения на ЭВМ.
Распечатка к задаче № 4.
Module/submodule: Linear Programming
Problem title: ( untitled)
Objective: Maximize
Results -----------------

5. Решить транспортную задачу
ai = (300, 250, 150, 150)
bj = (145, 195, 180, 140, 190)
9 4 8 7 4
7 7 3 9 6
9 3 7 6 5
4 6 5 4 6
Ответы: 1)Zmin=712; 2)Zmin=1260; 3)Zmin=3840; 4)Zmin=2120; 5)Zmin=3475.

6. По сетевому графику найти ранний и поздний сроки свершения событий, определить критический путь и его длину, найти свободный и полный резерв времени работ.

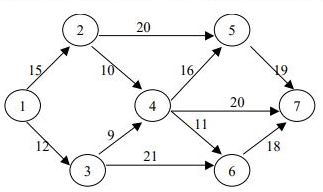
Ответы длины критического пути:
1) 70; 2) 85; 3) 90; 4) 105; 5) 60.
7. В области решений системы неравенств определить глобальные экстремумы
функций. Решить задачу графическим способом Z=2-х1-х2/2

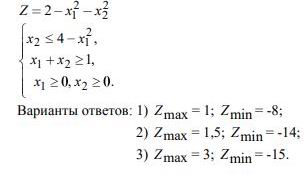
Варианты ответов: 1)Zmax= 1; Zmin= -8; 2)Zmax= 1,5; Zmin= -14; 3)Zmax= 3; Zmin= -15.

Вариант 8
1. Если исходная задача имеет ..., то и двойственная ей задача имеет …
2. Найти два опорных решения системы уравнений.

Ответы первого опорного решения:0X1= (0; 0; 7; 2; 10; 9); 0X1= (7; 0; 0; 2; 0;10); 3)0X1= (7; 2; 10; 0; 0; 0); 4)0X1 = (0; 2; 7; 10; 0; 0); 5)0X1= (3; 2; 7; 0; 0; 0).

3. Решить исходную задачу симплексным методом, составить к ней модель двойственной задачи, найти оптимальный план двойственной задачи. Z=2x1+x2+x3_max

4. Предприятие имеет 4 вида ресурса и выпускает 4 вида продукции. Исходные условия задачи заданы в таблице.
Таблица данных Вид ресурса Затраты ресурсов на 1 единицу продукции Запас
                             1 2 3 4
В1                         1 6 0 2 250
В2                         3 2 3 4 300
В3                         1 0 5 1 240
В4                         4 5 2 3 350
Цена 1 единицы
продукции                    3 5 7 3
Найти оптимальный план выпуска продукции при котором прибыль от реализации продукции будет оптимальной.
Требуется:
а) Составить математическую модель исходной и двойственной задач.
б) Записать решение исходной задачи
в) Записать решение двойственной
г) Проанализировать решение задачи с помощью свойств двойственных оценок (4 свойства).
д) Как изменится , целевая функция в оптимальном плане , если продать 100 единиц третьего ресурса.
Ответы:
1) уменьшится на 128,92.
2) уменьшится на 27,71.
3) уменьшится на 60,24.
4) увеличится на 128,92.
5) увеличится на 100.
К задаче прилагается распечатка решения на ЭВМ.
Распечатка к задаче № 4.
Module/submodule: Linear Programming
Problem title: ( untitled)
Objective: Maximize
Results -----------------

5. Решить транспортную задачу
ai = (210, 200, 200, 290)
bj = (210, 150, 170, 200, 200)
9 11 12 10 8
5 10 8 9 6
12 14 8 12 7
7 6 7 10 5
Ответы: 1)Zmin=3140; 2)Zmin=4820; 3)Zmin=4930; 4)Zmin=7420; 5)Zmin=6200.

6. По сетевому графику вычислить ранний и поздний сроки свершения событий, определить критический путь и его длину, найти свободный и полный резерв времени работ.

Ответы длины критического пути:
1) 80; 2) 95; 3) 100; 4) 87; 5) 98.
7. В области решений системы неравенств определить глобальные экстремумы функций. Решить задачу графическим способом. Z=(х1-3)2+(х2-2)2

Варианты ответов: 1)Zmax= 13; Zmin= 0; 2)Zmax= 8;Zmin= 2; 3)Zmax= 8; Zmin= -1.

Вариант 9
1. Если в оптимальном плане ресурс используется ... и оценка единицы этого ресурса…, то такой ресурс называют дефицитным.
2. Найти два опорных решения системы .

Ответы первого опорного решения: 1)0X1= (0; 2; 1; 3; 0); 0X1= (2; 1; 3; 0; 0) 3)0X1= (2; 1; 0; 0; 3); 4)0X1= (1; 3; 2; 0; 0); 5)0X1= (1; 0; 0; 3; 2).
3. Решить исходную задачу симплексным методом, составить к ней модель двойственной задачи, найти оптимальный план двойственной задачи. Z=-x1-x2-x3_max

4. Предприятие имеет 4 вида ресурса и выпускает 4 вида продукции. Исходные условия задачи заданы в таблице.
Таблица данных
Вид ресурса Затраты ресурсов на 1 единицу продукции Запас ресурса
                      1 2 3 4
В1                  5 3 2 4 800
В2                  2 4 6 5 720
В3                  5 2 0 1 650
В4                  3 4 1 2 700
Цена 1 единицы
продукции            9 4 6 3
Найти оптимальный план выпуска продукции при котором прибыль от реализации продукции будет максимальной.
Требуется:
а) Составить математическую модель исходной и двойственной задач.
б) Записать решение исходной задачи
в) Записать решение двойственной
г) Проанализировать решение задачи с помощью свойств двойственных оценок .
д) Как изменится , целевая функция в оптимальном плане , если продать 300 единиц первого ресурса.
Ответы:
1) уменьшится на 235,67.
2) уменьшится на 484,62.
3) увеличится на 200,29.
4) увеличится на 38,46.
5) уменьшится на 300.
К задаче прилагается распечатка решения на ЭВМ.
Распечатка к задаче № 4.
Module/submodule: Linear Programming
Problem title: ( untitled)
Objective: Maximize
Results -----------------

5. Решить транспортную задачу
ai = (100, 120, 80, 120)
bj = (60, 100, 95, 125, 40)
4 5 3 4 7
3 6 2 1 6
5 4 7 3 9
2 3 1 9 6
Ответы: 1)Zmin=1125; 2)Zmin=2120; 3)Zmin=1720; 4)Zmin=2120; 5)Zmin=175.
6. По сетевому графику вычислить ранний и поздний сроки свершения событий, определить критический путь и его длину, найти свободный и полный резерв времени работы (2-5).
Ответы длины критического пути:
1) 75; 2) 57; 3) 60; 4) 70; 5) 66.

7. В области решений системы неравенств определить глобальные экстремумы функций. Решить задачу графическим способом. Z=х1/2+х2/2-2х1-10х2+26
Варианты ответов: 1)Zmax= 26;Zmin=5/9/5; 2)Zmax= 30;Zmin= 4; 3)Zmax= 34;Zmin= 5

Вариант 10
1. Оценка единицы i-го ресурса (yi) показывает, на сколько изменится целевая функция в оптимальном плане , если ... изменится на ...
2. Найти два опорных решения системы. х1+2х2=1
Ответы первого опорного решения: 1)0X1= (0; 1; 5; 4; 2); 2)0X1= (1; 0; 2; 0; 4); 3)0X1= (2; 3; 1;0;0); 4)0X1= (0; 0; 1; 4; 2); 5)0X1= (1; 0; 0; 4; 2).
3. Решить исходную задачу симплексным методом, составить к ней модель двойственной задачи, найти оптимальный план двойственной задачи. Z=4x1+12x2_max

4. Предприятие имеет 4 вида ресурса и выпускает 4 вида продукции. Исходные условия задачи заданы в таблице.
Таблица данных
Вид ресурса    Затраты ресурсов на 1 единицу продукции Запас ресурса
                                       1 2 3 4
В1                                  5 3 0 2 550
В2                                  3 3 1 2 500
В3                                  3 4 2 1 650
В4                                  2 3 5 6 750
Цена 1 единицы
продукции                             4 4 5 8
Найти оптимальный план выпуска продукции при котором прибыль от реализации продукции будет максимальной.
Требуется:
а) Составить математическую модель исходной и двойственной задач.
б) Записать оптимальное решение исходной задачи
в) Записать оптимальное решение двойственной
г) Проанализировать решение задачи с помощью свойств двойственных оценок.
д) Как изменится , целевая функция в оптимальном плане, если дополнительно
приобрести 500 единиц четвертого ресурса. Если считать что увеличение целевой функции.
Ответы: 1)Zmax=550; 2)Zmax=800; 3)Zmaх=900; 4)Zmax=625; Zmax=700.
К задаче прилогается распечатка решения на ЭВМ.
Распечатка к задаче № 4.
Module/submodule: Linear Programming
Problem title: ( untitled)
Objective: Maximize
Results -----------------

5. Решить транспортную задачу
ai = (150, 100, 150, 100)
bj = (100, 70, 130, 110, 90)
3 9 5 4 3
8 3 4 2 5
2 6 4 5 4
5 6 8 7 2
Ответы: 1)Zmin=1800; 2)Zmin=1670; 3)Zmin=7920; 4)Zmin=6120; 5)Zmax=2450.

6. По сетевому графику вычислить ранний и поздний сроки свершения событий, определить критический путь и его длину, найти свободный и полный резерв времени работы (2-5).
Ответы длины критического пути: 1) 60; 2) 75; 3) 64; 4) 58; 5) 57.

7. В области решений системы неравенств определить глобальные экстремумы функций. Решить задачу графическим способом. Z=(х1-3)2+(х2-4)2
Варианты ответов:
1)Zmax= 25;Zmin= 1/203/841
2)Zmax= 20;Zmin=2/13/16
3)Zmax= 26;Zmin=1/19/81.